General Relativity: How Einstein Redefined Gravity

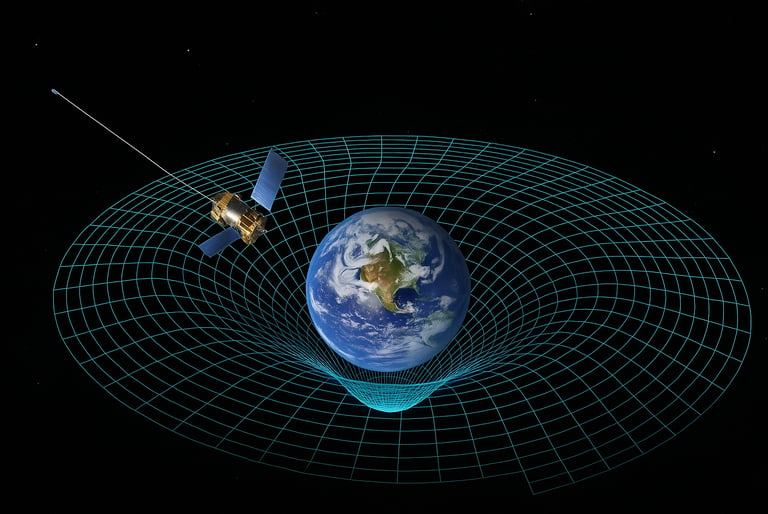
Gravity is the quiet pull that shapes the world around us — the reason rain pours, rivers flow downhill, and oceans rise and fall with the Moon’s gaze. It is so familiar, so ever-present, that we rarely pause to question its strangeness. Yet this gentle force that tugs at our bodies also binds planets in orbit, anchors moons to worlds, and shepherds entire galaxies in colossal, spiralling dances. Stretching across the vast expanse of the universe, gravity holds galaxy clusters together like threads in a cosmic drapery. It gathers scattered dust into stars, stars into galaxies, galaxies into clusters — as if the universe, at every scale, is engaged in a quiet yearning, a tendency toward closeness. In a cosmos filled with motion and change, gravity is the enduring call that draws everything toward everything else.

For much of human history, gravity was taken for granted as a natural part of existence. Some of the earliest discussions on gravity began with ancient philosophers such as Aristotle, who proposed that heavier objects fall faster than lighter ones. This belief persisted for over two millennia until Galileo demonstrated, in the 16th century, that objects accelerate uniformly under gravity, regardless of their mass, laying the groundwork for the Weak Equivalence Principle1 (WEP). This radical shift in thought reached its full flowering with Newton and his famous Philosophiæ Naturalis Principia Mathematica2 in 1687. Perhaps the most profound inclusion in this work is the Universal Law of Gravitation, which describes gravity as a force by stating that every massive particle attracts every other massive particle in the universe with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between their centres of mass, with separated masses acting as if all their mass were concentrated at their centers. This takes the famous mathematical form, known as the inverse-square law:

Newton’s theory, for all its elegance and success, fell short of explaining why gravity worked. It described the force precisely but offered no insight into its underlying mechanism. Gravity was treated as an invisible influence acting instantaneously across space – a notion that later came to be seen as a violation of causality, since it implied that changes in one mass could affect another without any time delay or intermediary. Furthermore, Newtonian gravity assumed that a body’s gravitational interaction was independent of its state of motion. While this may have seemed intuitive at the time, it stood in sharp contrast to electrodynamics, the other great theory of classical physics, where the behaviour of charged particles and fields does depend on their motion. Something was missing. There were signs that gravity, as understood then, was incomplete, and a deeper, more consistent explanation was needed.

One of the first major cracks in the Newtonian framework appeared in 1859, when Urbain Le Verrier reported an anomaly in the orbit of Mercury. Careful analysis of Mercury’s transits across the Sun revealed that the planet’s perihelion was advancing at a rate that exceeded predictions by 43 arcseconds per tropical century (initially estimated at 38 arcseconds). Newtonian mechanics could not account for this discrepancy. Several ad hoc explanations were proposed, including the existence of a hypothetical inner planet named Vulcan3, whose gravitational pull might have accounted for the unexplained shift. However, no observational evidence of Vulcan ever emerged, and the limitations of Newtonian gravity started to become apparent.

The bending of spacetime around a massive object is the central idea of General Relativity.

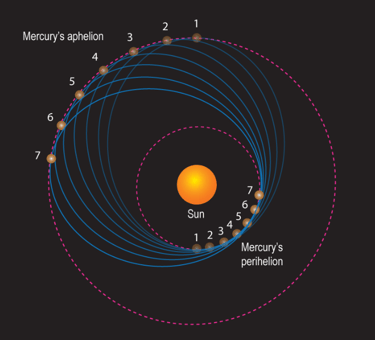
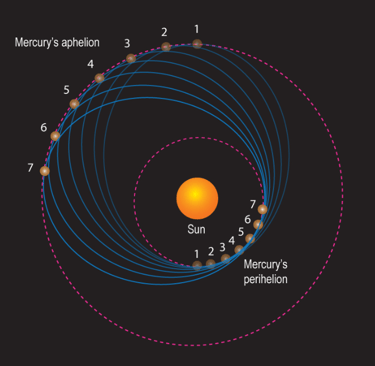
As Mercury revolves around the Sun, its orbit gradually shifts or precesses. This means the locations of its closest and farthest points from the Sun—perihelion and aphelion—slowly rotate around the Sun over time. While Newtonian gravity explains most of this motion, it falls short of accounting for the full effect. General relativity, however, accurately describes the complete behaviour. Note: the orbit's eccentricity is highly exaggerated in this illustration.

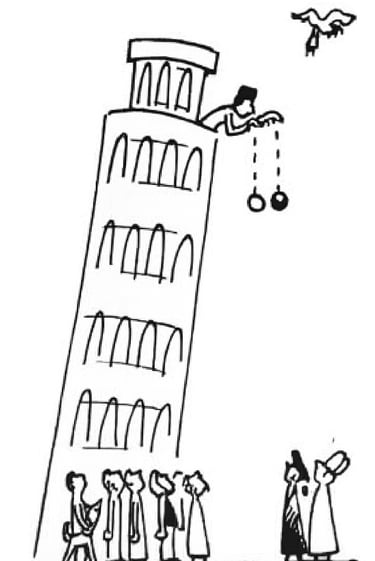
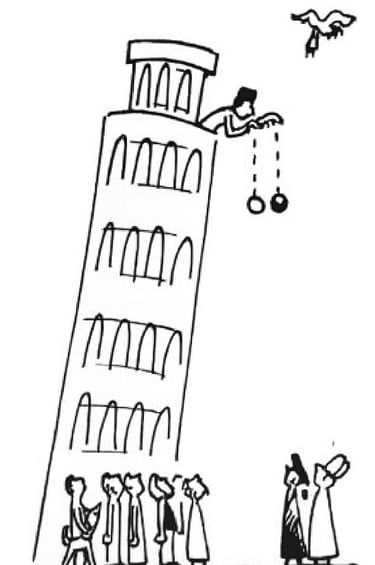
The illustration depicts Galileo Galilei demonstrating what is now known as the Weak Equivalence Principle (WEP)—the idea that all objects fall with the same acceleration regardless of their mass or composition. According to a famous account by his student Vincenzo Viviani, Galileo dropped spheres of unequal mass but identical material from the Leaning Tower of Pisa sometime between 1589 and 1592. The experiment, meant to disprove Aristotle’s theory that heavier objects fall faster, showed that both fell at the same rate. While it remains uncertain whether Galileo actually performed this test or merely proposed it as a thought experiment, the principle he illustrated remains a cornerstone of modern physics.

The start of the 20th century marked a fresh revolution in physics, kick-started by Einstein’s Special Theory of Relativity (STR) in 1905. STR was founded on two fundamental principles – the invariance of physical laws across inertial frames and the constancy of the speed of light in a vacuum. The latter was particularly revolutionary as it eliminated the notion of absolute time or simultaneity. Governed by the Lorentz transformation equations, the consequences of STR include strange phenomena like time dilation and length contraction.

While the central idea behind STR was profound, its applicability was limited to inertial frames. To appreciate this constraint, we must first understand a consequence of the WEP. Imagine an observer trapped in a box in free space4. Suppose that the top of the box is attached to a rope which is controlled by an entity, and that the observer is supplied with apparatus freely floating in the space inside the box. The observer now experiences weightlessness5. Let the entity begin pulling the rope at a constant rate, imparting a uniform acceleration to the box. The observer then begins feeling a pull towards the floor of the box, which exerts a reactive force on the observer, causing him to accelerate with the box. All the apparatus in the box, irrespective of mass or composition, appears to the observer to fall at a uniform rate. Given that the WEP implies equal gravitational acceleration to all objects in a gravitational field, the observer can reasonably and logically interpret the box as being in a uniform gravitational field acting in the direction of the floor. However, to an observer far away, it appears that the box is accelerating uniformly upwards. This implies that a uniform gravitational field in one coordinate frame can be replaced by uniform acceleration of another coordinate frame. In this sense, an observer in a gravitational field is non-inertial, so special relativity does not hold.

Imagine two identical bowls filled with water. If there was steam rising only from one of them, it would be strange. But if you noticed a burning flame underneath the steaming bowl, the surprise would vanish, even if you’ve seen neither steam nor flame before, for the physical conditions of the two bowls are distinct – you attribute the burning flame as the cause of the rising steam, even if you have no idea about the physical mechanism taking place. Analogously, there is nothing physically distinguishable between the experiences of the observer in the box and the observer in free space. Hence, we must conclude that there is no fundamental difference between a uniform gravitational field and a uniformly accelerating frame of reference. Therefore, the laws of physics should not depend on the state of motion of any reference frame; only such a set of laws could be called 'general'.

Einstein was particularly uncomfortable with the idea of physics being fundamentally different for an observer in a gravitational field, as was apparent from the Newtonian standpoint. He countered it with a thought experiment, which he would later describe jokingly as the happiest thought of his life. Imagine a man falling from the roof of a building. To him, he is the centre of the universe and the ground beneath him, along with everything else on the ground, is uniformly accelerating upwards. He feels weightless, as if gravity has vanished. However, anything that is also freely falling appears to him to be at rest.

This suggested the interpretation that the falling man was a true inertial observer, while everything attached to the ground was accelerating. As much as this interpretation may seem off, it is greatly profound and more powerful than the general belief. We have already established the equivalence between a uniform gravitational field and a uniformly accelerating reference frame. It must not be falsely assumed that every gravitational field can be replaced by an accelerating frame. Most gravitational fields, such as the Earth’s, which is directed radially towards the centre, cannot be replaced by any accelerating frame in its entirety. However, the gravitational field in a sufficiently small region of the Earth can be assumed to be uniform, and a corresponding accelerating frame can be found. Thus, every local gravitational field can be replaced by an accelerating frame. But a freely falling observer in a local gravitational field does not experience gravity, as illustrated by Einstein’s thought experiment. It is therefore natural to consider freely falling frames as the true inertial frames in the presence of gravity. In contrast, an observer who remains at rest in a gravitational field, and thus feels the force of gravity, is actually in an accelerated frame, making it non-inertial. This reversal of perspective is central to General Relativity and, as it will turn out, its description of gravity.

Having understood this shift in perspective, we can alternatively summarise the WEP as follows: For small enough length scales, it is not possible to distinguish between the presence of a gravitational acceleration and an accelerated reference frame. To understand why we must limit the WEP to small length scales, we shall consider how gravity changes as we move through space. We know from Newton’s inverse square law of gravity that the strength of the gravitational field drops as we move farther away from the source. This means, in principle, that your feet, which are closer to the ground, are pulled slightly more strongly than your head. Moreover, in radial gravitational fields, such as the Earth’s, the field lines are not parallel but converge at a central point. This implies that any object in Earth’s gravitational field will experience a compression in addition to an inward pull. While these effects are negligible on small scales, they are noticeable across the Earth’s diameter as oceanic tides. No accelerated reference frame can create the illusion of a tidal force. The equivalence only holds when the effects of gravity, such as tides, become unnoticeable on small scales. How small this size is depends on the precision of the measurements that can be made.

Einstein extended this principle to include that the outcome of any local, non-gravitational experiment is independent of the experimental apparatus’ velocity relative to the gravitational field and is independent of where and when in the gravitational field the experiment is carried out. These two additional constraints – the independence of the outcome on the relative velocity (Lorentz invariance), and the independence of the place of the outcome (positional invariance) – make the Einstein Equivalence Principle (EEP) a stronger version of the WEP. The modern version of this, known as the Strong Equivalence Principle (SEP), applies the same constraints as EEP, but allows freely falling bodies to be massive self-gravitating bodies, such as stars and planets, in addition to test particles. Essentially, the SEP posits that the laws of physics must be the same for all observers, whether accelerated or not. The SEP could be violated if strongly self-gravitating bodies fell differently, perhaps due to higher-order terms in the scalar field, than test particles. However, all experiments performed to date are in agreement with the SEP, and general relativity is the only theory that satisfies this principle.

The concept of spacetime as a four-dimensional continuum of events was first introduced in the theory of Special Relativity. In the absence of mass and energy, this spacetime is flat, and objects move along straight-line paths, as dictated by Newton’s First Law. However, to understand gravity within the framework of General Relativity, we must examine how massive objects influence the geometry of spacetime itself.

We have seen that accelerating frames can mimic the effects of gravitational fields locally, but this equivalence breaks down over larger regions of spacetime. In such cases, observers begin to detect tidal effects which cannot be explained by uniform acceleration alone. This means that different observers cannot always agree on the equivalence of gravitation and acceleration – there is no global accelerating frame that can replace gravity everywhere.

At the same time, one of the foundational principles of General Relativity, often called the principle of relativity, is that the laws of physics are locally identical for all observers, regardless of their state of motion. This idea is formalised in the principle of general covariance, which asserts that physical laws must take the same mathematical form in all coordinate systems, inertial or not.

In a truly flat spacetime, any differences in gravitational effects between observers should be reconcilable through a change of coordinates. But in reality, this is not always possible. The presence of mass or energy causes observers to experience genuinely different gravitational phenomena that cannot be transformed away. For instance, two test particles dropped from the same height get closer as they fall closer to the Earth due to a slight difference in the gravitational pull at each particle’s location – the tidal effect. Thus, the only way to preserve the equivalence principle and the universality of physical laws is to give up the idea of flat spacetime for a curved one. In this curved spacetime, gravity can be locally replaced by accelerating frames everywhere, but each frame will have a different acceleration.

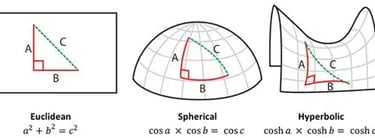
The central idea of General Relativity is that gravitational effects are consequences of objects following natural trajectories in curved spacetime. To understand this, we must first understand how curved geometry is different from flat geometry. Any geometry can be classified as Euclidean, elliptic, or hyperbolic based on its flatness. A flat geometry assumes five postulates, known as Euclid’s postulates. Of these, it is the fifth postulate, which describes parallelism, that separates non-Euclidean geometries from flat geometry. The original formulation of this postulate is as follows:

If a straight line falls on two straight lines in such a manner that the interior angles on the same side are together less than two right angles, then the straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.

Essentially, this postulate states that parallel lines never meet – they are equidistant throughout their lengths. Here, parallel lines are any pair of lines with a common perpendicular. While this seems obvious, this is not true in non-Euclidean geometries.

In an elliptic geometry, parallel lines are not equidistant throughout their lengths. Instead, they always meet at exactly two points. Any closed geometry, such as the spherical surface of the Earth, meets this description. The longitudes are parallel lines running across the Earth’s surface and meet at the two poles. Likewise, parallel lines are not equidistant in a hyperbolic, or open, geometry. However, they are not bound to meet and may diverge instead.

Another way to test for curvature is to sum the interior angles of a triangle. In a closed geometry, the sum of the interior angles of a triangle is more than 180 degrees, whereas this sum is less than 180 degrees in an open geometry. If you tried to make this measurement on a small patch of land on Earth, you would measure the sum of the angles to be (close to) 180 degrees. This indicates that the Earth is locally flat, which is justified given its much larger size compared to us.

Credit: Dr. Mark Liu

The ‘natural path’ or inertial trajectory followed by a test mass in spacetime is referred to as a geodesic6. This path is determined by the Einstein field equations7 (EFE) and depends on the mass of the gravitating object as well as the velocity of the test mass. The field equations are tensor equations which relate local spacetime curvature to the local energy, momentum, and stress within that spacetime. The EFE relates the spacetime geometry to the distribution of momentum, energy, and stress in that region of spacetime. This is analogous to how Maxwell’s equations relate electromagnetic fields to the distribution of charges and currents in space. The geometric and causal structure – such as the notions of time, distance, and volume – is captured mathematically by the metric tensor. On the other hand, the curvature of spacetime is captured by the Einstein tensor, which is an inverted Ricci tensor. The EFE is a set of non-linear partial differential equations, the solutions of which are components of the metric tensor. The geodesics of particles or radiation are calculated using the geodesic equation.

Matter acts on spacetime, telling it how to curve. Spacetime acts on matter, telling it how to move.

A crude but helpful way to picture gravity as spacetime curvature is to think of two particles moving along two longitudes on Earth, from the equator to the North Pole. Here, think of the longitudes as geodesics of the particles. Although the particles move along ‘straight’ paths, the curvature of spacetime (here, the Earth’s curvature) causes them to move closer together until they eventually meet (at the North Pole). Spacetime curvature affects matter in a similar way. While particles and radiation move along their geodesics, the surrounding matter and energy curve spacetime in a concave fashion, causing these geodesics to converge. This effect appears to us as gravitational attraction.

This abstract idea can be visualised by a tabletop experiment. Stretch out a rubber sheet and draw a grid throughout its surface. This sheet represents the spacetime fabric, and the gridlines represent the ‘straight’ geodesics. If you roll a marble along the sheet, it will continue rolling along a straight line. This is Newton’s first law, in flat space. Now, place a heavy object at the centre of the stretched sheet. This causes the central region of the sheet to dip. You can notice how the gridlines no longer appear straight, especially near the central object. This is analogous to how a massive object curves the surrounding spacetime.

To visualise the motion of objects under the influence of gravity, roll the same marble along a gridline. You will notice that it moves straight initially, but bends as it nears the dip. If you roll the marble with sufficient speed, and if the friction between the marble and the sheet is low enough, the marble will revolve around the central object. This captures the idea of how the Sun warps the surrounding spacetime, guiding the planets into elliptical orbits, not by pulling on them directly, but by shaping the paths they naturally follow.

The large ball (a star) bends the surrounding rubber sheet (spacetime), causing the smaller ball (a planet) to alter its course and follow the dip (geodesic).

Keep in mind, though, that this is merely a way to visualise gravity as the curvature of spacetime. The way the rubber sheet stretches isn’t exactly how geodesics are bent in real spacetime, though there is some conceptual resemblance. Most importantly, spacetime is 4-dimensional, whereas our experiment is on a 2-dimensional sheet. There is no physical well near a massive object such as a star that traps other objects when they get too close.

It may occur to you that curved spacetime need not necessarily imply converging paths. Yet, gravity is almost always attractive8. This just happens to be how our universe works. Spacetime curvature depends on the energy density of matter. For positive energy densities, which characterise all forms of matter and radiation, all solutions to the geodesic equation are converging ones. The concept of a negative energy density is generally forbidden in physics, partly because it appears unnatural, but mainly because it lacks any experimental evidence. From a mathematical standpoint, however, General Relativity does admit solutions with negative mass, which would curve spacetime differently and cause geodesics to diverge, giving rise to repulsive gravity. While these are theoretically possible, they remain speculative and are not known to occur in the real universe.

Now that we have a geometric interpretation of gravity, let us explore the behaviour of clocks and measuring rods in a spacetime containing matter. For simplicity, we shall consider a circular disc as our body of reference in a region of spacetime devoid of gravitational fields relative to this reference body, whose state of motion has been suitably chosen. The disc is now an inertial frame, and the laws of special relativity hold relative to this frame. Imagine two observers, one sitting eccentrically at the boundary and the other elsewhere in space, at rest relative to our body of reference. Now, let us set this disc into uniform rotation. The observer who is seated eccentrically on the disc is co-rotating with the disc and experiences a centrifugal force. However, this observer is unaware of any such motion and may perfectly regard the disc to be at rest based on the principle of relativity. To him, the force acting on him and all other bodies at rest relative to the reference body is a result of a gravitational field. To probe the nature of this field, he conducts experiments using clocks and measuring rods, attempting to define absolute notions of time and distance from within the rotating frame.

To start with, he places one of two identically constructed clocks at the centre and one at the edge, so that they are at rest relative to the rotating disc. As seen by the observer in space, the clock on the edge is in motion, whereas the clock at the centre has no velocity. According to special relativity, which still holds for this observer, the clock at the edge runs slower than the clock at the centre. Thus, on this circular disc, or in every gravitational field in general, a clock will run more quickly or less quickly depending on its position (in the gravitational field). Therefore, it is not possible to obtain a reasonable definition of time using clocks which are arranged at rest relative to a reference body.

Similarly, we are also posed with a challenge in obtaining a reasonable definition of distance using measuring rods. Let’s say the observer on the disc uses a standard measuring rod, which is short compared to the radius of the disc, to measure the disc’s circumference by placing the rod tangentially. As judged by the observer in space, this rod will have contracted due to its relative motion and will have to be stacked a greater number of times to span the circumference. Consequently, he will measure the circumference to be longer than what the observer co-rotating with the disc will measure. However, both observers measure the same diameter because the measuring rod will not contract relative to the inertial observer in space when arranged along a radius of the disc. Therefore, the inertial observer, upon dividing the circumference by the diameter, will obtain a value larger than pi (3.1415). This proves that the propositions of Euclidean geometry cannot be applied directly to a rotating disc, or a general gravitational field, for that matter. In a way, this suggests a non-Euclidean curved spacetime in the presence of a gravitating object.

It’s important to recognise that the presence of a gravitational field is relative to the observer. For example, someone standing on Earth's surface experiences what feels like a gravitational pull toward the centre of the planet. In contrast, an observer in free fall nearby would feel weightless and detect no such field. This illustrates a key insight of General Relativity: there is no absolute gravitational force field. Instead, the motion of objects is determined entirely by the curvature of spacetime itself – a geometric property that remains the same for all observers. Still, we often refer to gravity as a ‘force’ in everyday language, as it offers an intuitive way to understand its effects.

One of the conceptual difficulties with Newtonian gravity is its assumption of instantaneous action at a distance, which was implied by the inverse-square law — that a change in one object’s mass or position affects another object’s motion without any time delay. This notion violates the principle of causality, which states that information cannot travel faster than the speed of light. According to General Relativity, any change in the gravitational field propagates through spacetime as ripples — like a gravitational wave9 — at light speed. Thus, the influence of gravity travels at the speed of light, obeying causality. For instance, if the Sun were to suddenly vanish (ignoring physical impossibilities), Earth would continue orbiting as usual for about 8 minutes and 22 seconds — the time light takes to travel from the Sun to Earth. Only after this delay would the loss of the Sun's gravitational influence reach us, at which point Earth would drift off in a straight, tangential path. This alignment with causality is one of the most elegant and necessary features of General Relativity.

Much like any revolutionary theory, General Relativity was initially met with scepticism, both scientific and cultural. By the time Einstein proposed his geometric interpretation of gravity, the Newtonian worldview had become deeply entrenched. Even though the success of Special Relativity had brought Einstein recognition, the idea that gravity wasn’t a force but a consequence of curved spacetime — a novel concept in itself — felt counterintuitive. Within the scientific community, abandoning the familiar notion of force in favour of abstract geometry was a leap many were reluctant to take. Compounding this was the quantum revolution, which was generating far more excitement and tangible results at the time. As a result, General Relativity remained on the fringes until experimental evidence eventually compelled the world to take it seriously.

The first confirmation of General Relativity came in 1915 when Einstein successfully explained the long-standing anomaly in Mercury’s orbit. This was the same problem as mentioned in the beginning. While Newtonian mechanics could account for most of Mercury’s perihelion precession through the gravitational influence of other planets, there remained an unexplained discrepancy of 43 arcseconds per tropical century. Einstein demonstrated that this residual shift naturally arose from the curvature of spacetime described by his equations, necessitating no additional assumptions.

A more dramatic and public test followed in 1919, during a total solar eclipse. General Relativity predicted that massive bodies like the Sun should bend the path of light10 from distant stars, a phenomenon that would later be known as gravitational lensing. Einstein calculated that starlight grazing the Sun’s edge would be deflected by about 1.75 arcseconds. However, observing stars near the Sun is usually impossible due to the Sun’s brightness. The eclipse provided a rare opportunity. In the darkness of a total eclipse, astronomers could photograph stars near the solar disc and later compare their apparent positions to reference images taken at night.

Led by Arthur Eddington, two expeditions, one to Príncipe off the west coast of Africa and another to Brazil, set out to test this prediction. Despite technical issues and cloud cover, both teams managed to capture usable images, especially of the Hyades star cluster, which appeared near the Sun during the eclipse. After months of data analysis, Eddington and Dyson announced that the observed deflection matched Einstein’s prediction.

The results were front-page news. The confirmation of General Relativity not only validated Einstein’s revolutionary ideas but also made him a global celebrity overnight, capturing the public imagination in a way few scientific theories ever had.

One of the most intriguing questions in physics asks: What happens if you drop a charged particle in a gravitational field?

If it radiates electromagnetic energy — as Maxwell’s theory suggests for any accelerating charge — where does that energy come from? And if it doesn't — preserving the charge’s free-fall motion in general relativity — how can that be consistent with classical electrodynamics?

Einstein’s equivalence principle says a freely falling object feels no force — it’s just following the natural curves of spacetime. So, in its own frame, the charge shouldn’t radiate. Yet, a stationary observer might still claim it is accelerating and does radiate.

This leads to a remarkable realisation: radiation itself can be observer-dependent.

Although this thought experiment beautifully exposes tensions between relativity and electromagnetism, it hasn’t been tested — not because it's unimportant, but because the radiation (if any) would be far too weak to measure. Earth’s gravity is simply too gentle, and isolating a single falling charge with no external influences is beyond today’s tech.

Still, this paradox remains a powerful reminder: how we ask a question in physics can change the answer we get — and sometimes, what we "see" depends on where we stand.

GIF credit: GSJ

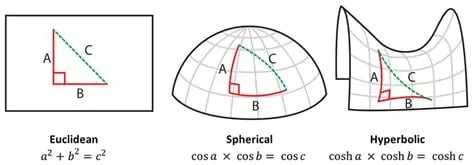
This illustration compares triangles drawn on flat, positively curved (closed), and negatively curved (open) geometries, showing how even basic shapes behave differently depending on the fabric of space itself.

As light from a distant star passes near the Sun, the curvature of spacetime bends its path. When we trace these bent rays back, the star appears slightly shifted from its true position.

Einstein’s General Relativity has since withstood countless experimental tests and remains the most accurate and consistent theory of gravity to date. One landmark test came in 1959 with the Pound-Rebka experiment, which confirmed the prediction that light climbing out of a gravitational field loses energy, resulting in a gravitational redshift11. Using gamma rays and the Mössbauer effect, which allows for extremely precise measurements of energy shifts, Pound and Rebka measured the change in frequency of gamma rays sent between the top and bottom of a tower at Harvard University. Despite the minute scale of the effect, their results matched the predictions of General Relativity to within 1% accuracy, providing one of the earliest high-precision confirmations of Einstein’s theory.

Incidentally, General Relativity also predicted the expansion of the universe12, which is one of the most profound discoveries in cosmology. When Einstein first formulated his field equations, he noticed that they naturally allowed for a dynamic universe that could expand or contract. However, at the time, the prevailing belief was that the universe was static and unchanging. To force his equations to yield a static solution, Einstein introduced an extra term known as the cosmological constant (Λ), which acted like a repulsive force to counterbalance gravity. But this adjustment was soon challenged by observational evidence. In the late 1920s, Edwin Hubble, after whom the Hubble Space Telescope was named, discovered that distant galaxies are redshifted, indicating they are moving away from us. This was clear evidence that the universe is expanding. Hubble’s findings confirmed what Einstein’s original equations had predicted all along. Upon learning this, Einstein reportedly referred to the introduction of the cosmological constant as the ‘greatest blunder’ of his life. Ironically, modern cosmology has revived the cosmological constant in the context of dark energy13, which is believed to drive the current accelerated expansion of the universe.

General Relativity remains a specialised branch of theoretical physics, known for its complex and mathematically demanding field equations, which rarely yield exact solutions. In practice, most astrophysical problems, and even space missions, rely on the simpler Newtonian framework, as relativistic effects are negligible under ordinary conditions. Only in extreme environments, such as near compact objects like black holes and neutron stars, or in the very early universe, do the predictions of General Relativity significantly diverge from Newtonian gravity and become essential for accurate descriptions.

Nevertheless, it plays a crucial role in modern life. The most prominent example is the Global Positioning System (GPS), where satellite clocks tick faster than those on Earth due to weaker gravity. This is due to gravitational time dilation14, an effect predicted by GR, and accounting for this is essential for accurate location tracking. For context, satellite clocks tick about 38 microseconds faster per day than Earth clocks (45 microseconds gained due to weaker gravity, minus 7 lost due to motion). While 38 microseconds may seem small, GPS relies on nanosecond-level precision. Without accounting for relativistic corrections, a GPS fix would become inaccurate within just 2 minutes, and errors would build up at a rate of around 10 kilometres per day, making it utterly useless! Telecommunications, financial networks, and power grids also rely on synchronised clocks that must correct for relativistic time dilation to maintain precision. Even atomic clocks15 on Earth show measurable differences in time at different altitudes, a direct result of GR. From satellite navigation to high-precision instruments, Einstein’s theory subtly but powerfully underpins much of the technology we depend on today.

Today, General Relativity and Quantum Mechanics stand as the twin pillars of modern physics. While Quantum Mechanics explains three of the four fundamental forces – the electromagnetic, strong, and weak interactions – with remarkable accuracy, gravity is described solely by Einstein’s classical framework. Yet these two theories are fundamentally incompatible. General Relativity paints a smooth, continuous, and deterministic picture of space and time, while Quantum Mechanics thrives on intrinsic randomness and uncertainties. Nowhere is this conflict more striking than in the heart of black holes or at the birth of the universe (the Big Bang). Ironically, these singularities are predicted by General Relativity itself, as if telling us that the theory is not complete. Physicists believe a quantum theory of gravity must emerge to explain such extremes, but despite promising attempts like String Theory and Loop Quantum Gravity, a full reconciliation remains elusive. A century after Einstein’s revolution, the quest for a unified theory – dubbed ‘The Theory of Everything’ – continues16, driven by the very spirit of curiosity and consistency that gave birth to General Relativity itself.

The story of General Relativity doesn’t end here. While the theory was born from the revolutionary insights of Einstein, its implications extend far beyond the elegance of its conception. Phenomena such as gravitational lensing, gravitational redshift, time dilation, and frame dragging, once thought of as purely theoretical predictions, now play a vital role in our understanding of the universe at its grandest scales. Each of these deserves a deeper dive of its own. Until then, the next time you catch a falling object or spill your coffee, remember – it’s not some spooky, invisible force pulling things down, but matter moving along the natural paths, or geodesics, carved out by the curvature of spacetime.

Tell Me More!

1) Weak equivalence principle

Consider two bodies, one of mass m and the other of mass M, separated by a distance r. The magnitude of acceleration ag gravitational force between them is given by

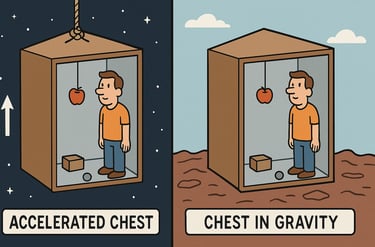
This split-screen image illustrates the equivalence principle. On the left, a person stands inside a closed box (like an elevator) being accelerated upward in deep space—stars visible outside. On the right, the same scene is shown on a planet’s surface under gravity. Both interiors look identical: the person stands normally, an apple hangs from a string, and objects rest on the floor. The visual conveys that the effects of acceleration and gravity are locally indistinguishable.

It has been tested experimentally, up to one part in 10^12, that the ratio mg/mi is constant. This ratio is assumed to be unity for the sake of convenience (Had it been chosen to be something else, the value of the gravitational constant G would have changed accordingly). The proportionality of the inertial and gravitational masses means that all objects, regardless of their composition, experience the same gravitational acceleration at a given location. This result, which is essentially the constancy of mg/mi, is often referred to as the weak equivalence principle.

2) Philosophiæ Naturalis Principia Mathematica

Often referred to simply as the Principia, this seminal work by Isaac Newton, published in 1687, laid the foundations of classical mechanics. In it, Newton formulated the laws of motion and universal gravitation, providing a unified mathematical framework to describe the motion of celestial and terrestrial bodies. The Principia remained the dominant scientific worldview for over two centuries, shaping our understanding of space, time, and force, until it was ultimately superseded by Einstein’s theory of General Relativity in the 20th century.

3) Neptune, then Vulcan?

Much like Mercury’s unexplained precession, astronomers in the 19th century noticed that Uranus's orbit didn’t match predictions based on Newtonian gravity. They hypothesised that an unseen planet was perturbing its motion. This led to targeted observations, and Neptune was discovered in 1846 exactly where predicted. Encouraged by this success, astronomers applied the same reasoning to Mercury’s unexplained orbital motion and proposed a closer-in planet named Vulcan. Though widely searched for, Vulcan was never found. Later, Einstein’s General Relativity explained Mercury’s motion without needing a new planet.

4) Free space

A theoretical region of space that contains no matter and no electromagnetic fields. It serves as an idealised backdrop for formulating physical laws, such as Maxwell’s equations and Einstein’s field equations. Free space provides a reference state, free from any disturbances, against which the presence of mass, energy, or fields can be measured and their effects analysed. Despite being an abstraction, it plays a crucial role in defining constants like the speed of light in a vacuum.

5) Weightlessness

This is the condition in which a person or object experiences no apparent weight. This occurs when they are in free fall, accelerating at the same rate as gravity, such as in orbit around Earth. Although gravity is still present, there is no normal force pushing back – what we perceive as weight – leading to a sensation of floating. Astronauts experience weightlessness aboard spacecraft, and train for it using neutral buoyancy pools on Earth, where they are submerged in water to simulate the feeling and effects of microgravity.

6) Geodesic

A geodesic is a curve that acts as a distance minimiser between two points on a surface locally, like a straight line on a plane. In a Riemannian manifold, a geodesic can also be seen as the path that minimises an energy-like quantity over time. They are of particular importance in General Relativity, where the motion of freely falling test particles is described by time-like geodesics.

Consider aeroplane routes between continents. Although they may appear curved on a flat map, they actually follow geodesics (great circles) on the curved surface of Earth. These are the shortest possible paths on a sphere.

While the appearance of m on both sides of the equation seems natural, a close inspection shows that the term m represents different quantities on either side. On the left, m represents the inertial mass of the object, which is a measure of the object’s resistance to being accelerated, and exists even in the complete absence of gravity. On the right side, m represents the object’s gravitational charge, which is a measure of how strongly it is pulled in a gravitational field. There is no reason to suppose that these quantities are equal.

Accordingly, the correct form of the expression is

Now, the acceleration due to gravity is given by

Here, Rμν is the Ricci tensor, R is the scalar curvature (trace of Ricci tensor), gμν is the metric tensor, Λ is the cosmological constant, and Tμν denotes the stress-energy tensor. All other variables hold their usual meaning. If we introduce the Einstein tensor Gμν = Rμν - R gμν/2, then the EFE can be written as:

The Einstein Field Equations form a set of ten interrelated equations, each representing a component of a tensor equation. Together, they describe how spacetime is curved by matter and energy. These equations are non-linear and coupled, making them extremely difficult to solve exactly in most situations. However, under specific simplifying assumptions, exact solutions can be found. For instance, if we assume that the Einstein tensor vanishes everywhere, this means that the stress-energy tensor must also be zero, indicating a region of spacetime with no matter or energy. In this case, the EFE reduce to the vacuum Einstein equations. Solutions to these vacuum equations are known as vacuum solutions, and include important spacetimes like Minkowski (flat spacetime), Schwarzschild (describing a non-rotating black hole), and Kerr (a rotating black hole).

8) Repulsive gravity

Certain modified theories of gravitation include regimes where gravity becomes effectively repulsive at large scales, potentially explaining the observed cosmic acceleration. This can emerge in extensions of General Relativity like f(R) gravity, scalar-tensor theories, or models with higher-order curvature terms. Similar effects also arise in brane world or massive gravity scenarios, where geometric modifications to spacetime mimic a repulsive force.

9) Gravitational waves

Gravitational waves are ripples in the fabric of spacetime generated by the acceleration of mass, much like electromagnetic waves are produced by accelerating electric charges. First predicted by Einstein’s theory of General Relativity, they are an inevitable consequence of any asymmetric variation of a dynamic mass distribution. However, because gravity is an incredibly weak interaction, only the most violent and massive astrophysical events, such as merging black holes or neutron stars, produce waves strong enough to be detected.

This is not to say that the sudden disappearance of the Sun would create a gravitational wave. Such waves are produced only by asymmetric, accelerating masses. In contrast, the sudden removal of the Sun’s mass would cause a spherically symmetric change in the spacetime curvature — a shift in the static gravitational field, not a wave.

Gravitational waves propagate at the speed of light and interact very weakly with matter, allowing them to travel immense distances across the cosmos virtually unaltered. This makes them pristine messengers of the events that generated them, carrying with them subtle imprints of source dynamics and the structure of local spacetime.

The first direct detection of gravitational waves occurred in 2015 by the Laser Interferometer Gravitational-Wave Observatory (LIGO), confirming a key prediction of General Relativity and inaugurating a new era of observational astronomy. Detection involves measuring minuscule distortions in spacetime — smaller than a proton's width — using highly sensitive laser interferometers. Although countless gravitational waves ripple through the universe at all times, only those from the most energetic cataclysms rise above the threshold of current technology.

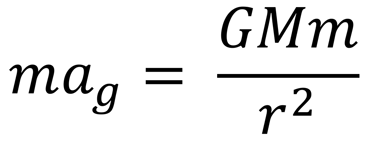
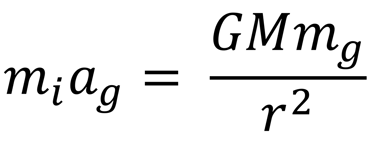
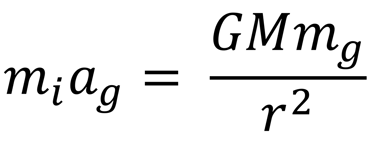
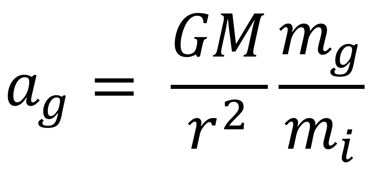
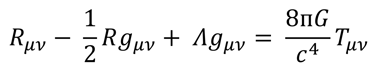
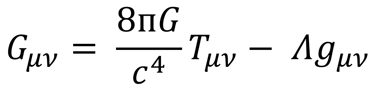
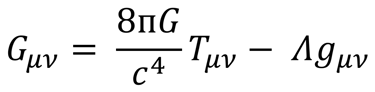
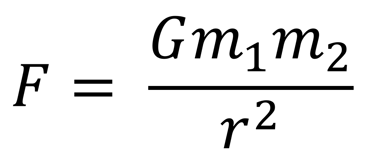
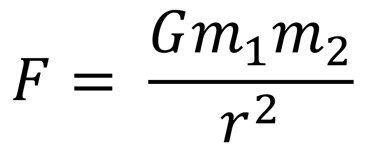
With this elegant formula, Newton united the motion of falling apples with the orbit of the Moon. This brought about a paradigm shift in the way we viewed physics – the laws of physics on Earth are the same as those elsewhere in the universe. Newton’s law of gravity explained planetary orbits with astonishing precision, and predicted satellite orbits, eclipses, and ocean tides. This version of universal gravity, widely used in applications even today, would remain unchallenged for over two centuries.

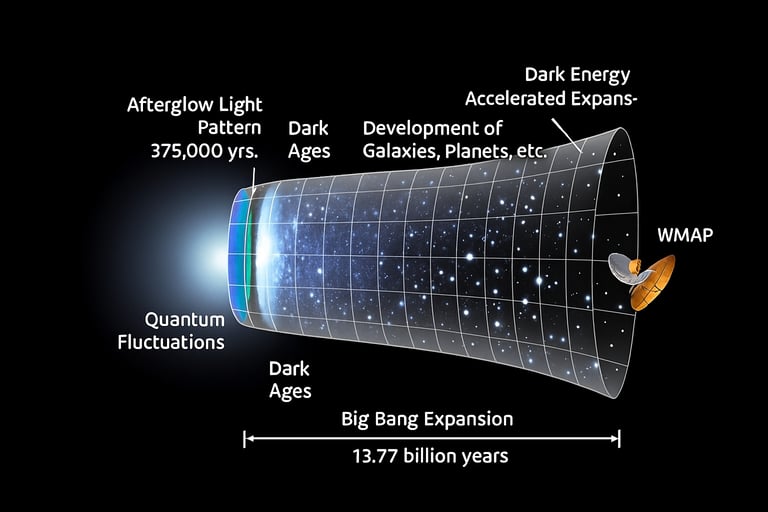
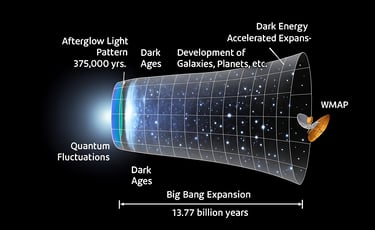
Courtesy: NASA

This illustration depicts the history and expansion of the universe from the moment of the Big Bang to the present day. The left side shows the initial quantum fluctuations and rapid inflation, followed by the afterglow light pattern (cosmic microwave background) about 375,000 years after the Big Bang. The timeline progresses through the “Dark Ages,” before the first stars formed around 400 million years in. As we move rightward, galaxies and planets begin to form. The cone widens, indicating the accelerating expansion of the universe driven by dark energy. A space telescope like WMAP appears near the modern end, observing the cosmos.

13) Dark energy

Dark energy is a mysterious form of energy believed to drive the accelerated expansion of the universe. Unlike matter or radiation, whose energy densities decrease as the universe expands – by the inverse cube or inverse fourth power of the scale factor, respectively – dark energy is thought to maintain a constant energy density over time, regardless of the volume in consideration. This uniformity allows it to dominate the universe's total energy budget, despite being less dense than ordinary or dark matter, making up about 68% of the cosmos. Acting in opposition to gravity on large scales, dark energy causes galaxies to move apart at an increasing rate. Its true nature remains one of the deepest puzzles in modern cosmology.

14) Gravitational time dilation

This refers to the slowing down of time in a strong gravitational field (strongly curved spacetime) as observed by a distant observer. This means that time passes differently for observers at different gravitational potentials. This effect has been demonstrated using initially synchronised atomic clocks at various altitudes and noting the differences in their times later on. Interestingly, the Earth’s core is in effect 2.5 years younger than its surface.

15) Atomic clocks

Atomic clocks are extremely precise timekeeping devices that rely on the natural vibration frequencies of atoms, most commonly caesium-133, to measure time. These clocks define the second in the International System of Units (SI) and are far more accurate than traditional mechanical or quartz clocks. For example, the best atomic clocks would drift by less than one second over the entire age of the universe (13.8 billion years). They are vital in applications like GPS, where exact timing ensures accurate positioning. Two key features of atomic clocks are their accuracy and stability, making them indispensable tools in both advanced scientific research and everyday technology.

16) Theory of everything

A Theory of Everything (TOE) is a proposed framework in physics that aims to unify all fundamental forces – gravity, electromagnetism, the strong nuclear force, and the weak nuclear force – into a single, consistent model. One of its central goals is to reconcile General Relativity, which describes gravity and large-scale structure, with Quantum Mechanics, which governs the behaviour of particles at microscopic scales. Some of the most prominent TOE candidates include String Theory, Loop Quantum Gravity (LQG), M-Theory, Grand Unified Theories (GUTs), and Holographic Models of the universe.

7) Einstein Field Equations

Einstein’s Field Equations (EFE) relate local spacetime curvature to local energy and momentum. These equations determine the metric tensor of a spacetime, given the configuration of stress-energy. The EFE are given as follows:

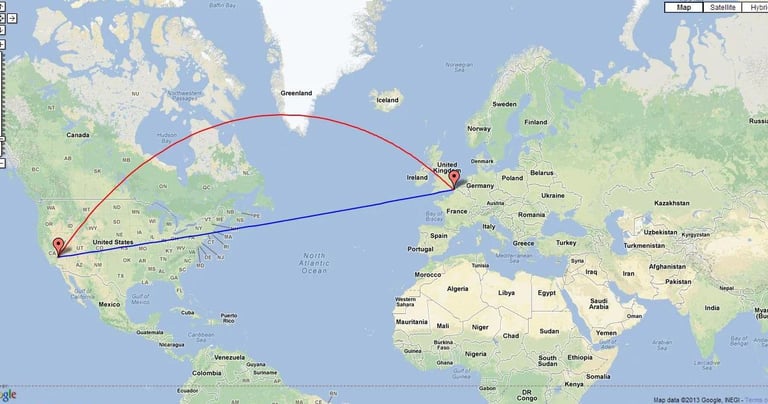
The blue line is the apparent shortest path between two points - California, USA (left) and London, UK (right) - on the flat Mercator projection of the Earth.

The red line, a great circle, is the true shortest path between the two points on Earth's spherical surface, followed by aircraft.

Courtesy: Google Maps

10) Gravitational light bending

It is not just massive objects that are affected by gravity. When light passes near a massive object, such as a star or galaxy, the spacetime around it is curved, causing the light’s path to bend. This bending isn’t due to a force acting on the photon, but rather the photon following a light-like geodesic in the curved geometry of spacetime itself.

11) Gravitational redshift

Electromagnetic radiation leaving the gravitational well of a massive object appears to be stretched to longer (redder) wavelengths, losing energy in the process. Gravitational redshift can be interpreted as a consequence of the equivalence principle and thereby, equivalent to the Doppler redshift.

12) Expansion of the universe

Astronomers, led by Edwin Hubble, observed that light from distant galaxies is redshifted, implying that the galaxies are moving away from us. Moreover, the galaxies appear to recede faster the farther they are. This is often interpreted as the expansion of the space between gravitationally bound regions. This doesn’t imply that space is expanding into anything or that there's an edge to the universe. Rather, it’s the fabric of space itself that's growing at cosmological scales.

Courtesy: NASA Goddard Space Flight Center/CI Lab

This striking image captures the dramatic aftermath of a black hole merger, visualised through rippling waves of warped spacetime. At the centre, two swirling black holes spiral inward and coalesce in a violent burst of gravitational energy. The newly formed black hole has slightly less mass than the sum of its progenitors—some of the mass has been converted into pure energy and radiated away as gravitational waves. These waves ripple outward (in deep blue concentric patterns), distorting the fabric of space like rings spreading across a cosmic pond, silently echoing the colossal event through the universe.